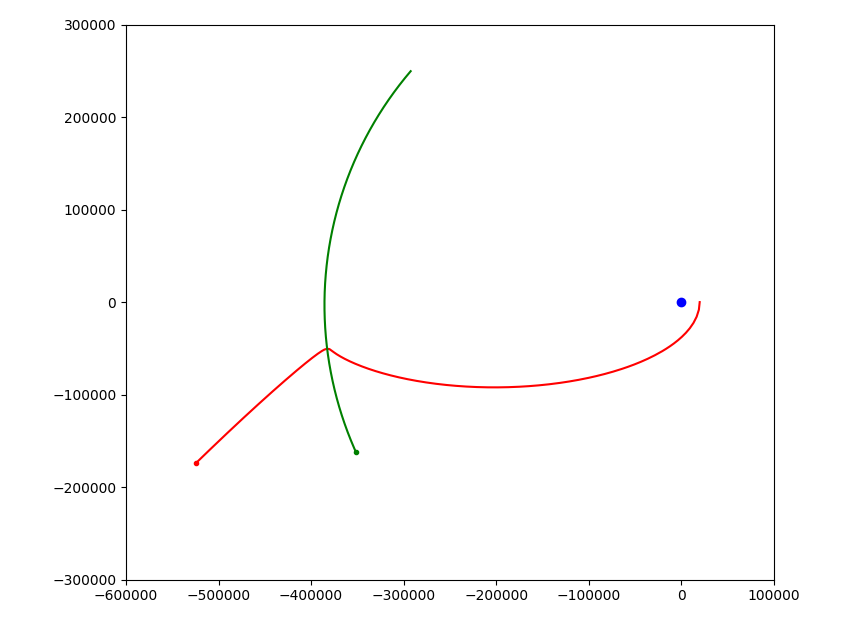
「パソコンで見る天体の動き」という本を参考にして、月と人工衛星のスイングバイをシミュレートしてみました。
二階微分方程式を解くので、ナイストレム法を使用しています。
# 地球を原点として,ナイストレム法でスイングバイシミュレーション
# 月と人工衛星
import numpy as np
import matplotlib.pyplot as plt
# --------------- 初期条件 --------------- #
# 刻み幅
h = 0.015625 # [day]
# 万有引力定数×惑星の質量(E:地球,M:月)
GE = 2.975537 * 10**15 # [km^3*day^-2]
GM = 3.659916 * 10**13 # [km^3*day^-2]
# 人工衛星
xs = 20000 # [km]
ys = 0
dxs_dt = 0 # [km/day]
# -6.17[km/s] を -6.17[km/day]に変換
dys_dt = -6.17 * 60 * 60 * 24
# 月
R = 384400 # [km]
theta = 2.435 # [rad]
dtheta_dt = 0.2302823 # [day^-1]
xm = R * np.cos(theta)
ym = R * np.sin(theta)
dxm_dt = -dtheta_dt * R * np.sin(theta)
dym_dt = dtheta_dt * R * np.cos(theta)
# ---------------------------------------- #
# 人工衛星の軌道の二階微分方程式(xs, ys で同じ)
def fs(xs, xm, rs, rm, rms):
return -GE*(xs/rs**3) + GM*((xm - xs)/rms**3 - xm/rm**3)
# 月の軌道の二階微分方程式(xs, ys で同じ)
def fm(xm, rm):
return -GE*(xm/rm**3)
# 座標を入れておくリスト
xs_list = [xs]
ys_list = [ys]
xm_list = [xm]
ym_list = [ym]
for i in range(360):
# 1次
rs = np.sqrt(xs**2 + ys**2)
rm = np.sqrt(xm**2 + ym**2)
rms = np.sqrt((xm - xs)**2 + (ym - ys)**2)
fs_x1 = fs(xs, xm, rs, rm, rms)
fs_y1 = fs(ys, ym, rs, rm, rms)
fm_x1 = fm(xm, rm)
fm_y1 = fm(ym, rm)
xs_1 = xs + 2/5*h*dxs_dt + 2/25 * h**2 * fs_x1
ys_1 = ys + 2/5*h*dys_dt + 2/25 * h**2 * fs_y1
xm_1 = xm + 2/5*h*dxm_dt + 2/25 * h**2 * fm_x1
ym_1 = ym + 2/5*h*dym_dt + 2/25 * h**2 * fm_y1
# 2次
rs = np.sqrt(xs_1**2 + ys_1**2)
rm = np.sqrt(xm_1**2 + ym_1**2)
rms = np.sqrt((xm_1 - xs_1)**2 + (ym_1 - ys_1)**2)
fs_x2 = fs(xs_1, xm_1, rs, rm, rms)
fs_y2 = fs(ys_1, ym_1, rs, rm, rms)
fm_x2 = fm(xm_1, rm)
fm_y2 = fm(ym_1, rm)
xs_2 = xs + 2/3*h*dxs_dt + 2/9 * h**2 * fs_x1
ys_2 = ys + 2/3*h*dys_dt + 2/9 * h**2 * fs_y1
xm_2 = xm + 2/3*h*dxm_dt + 2/9 * h**2 * fm_x1
ym_2 = ym + 2/3*h*dym_dt + 2/9 * h**2 * fm_y1
# 3次
rs = np.sqrt(xs_2**2 + ys_2**2)
rm = np.sqrt(xm_2**2 + ym_2**2)
rms = np.sqrt((xm_2 - xs_2)**2 + (ym_2 - ys_2)**2)
fs_x3 = fs(xs_2, xm_2, rs, rm, rms)
fs_y3 = fs(ys_2, ym_2, rs, rm, rms)
fm_x3 = fm(xm_2, rm)
fm_y3 = fm(ym_2, rm)
xs_3 = xs + 4/5*h*dxs_dt + 4/25 * h**2 * (fs_x1 + fs_x2)
ys_3 = ys + 4/5*h*dys_dt + 4/25 * h**2 * (fs_y1 + fs_y2)
xm_3 = xm + 4/5*h*dxm_dt + 4/25 * h**2 * (fm_x1 + fm_x2)
ym_3 = ym + 4/5*h*dym_dt + 4/25 * h**2 * (fm_y1 + fm_y2)
# 4次
rs = np.sqrt(xs_3**2 + ys_3**2)
rm = np.sqrt(xm_3**2 + ym_3**2)
rms = np.sqrt((xm_3 - xs_3)**2 + (ym_3 - ys_3)**2)
fs_x4 = fs(xs_3, xm_3, rs, rm, rms)
fs_y4 = fs(ys_3, ym_3, rs, rm, rms)
fm_x4 = fm(xm_3, rm)
fm_y4 = fm(ym_3, rm)
# 結果
xs += h * (dxs_dt + (h/192)*(23*fs_x1 + 75*fs_x2 - 27*fs_x3 + 25*fs_x4))
ys += h * (dys_dt + (h/192)*(23*fs_y1 + 75*fs_y2 - 27*fs_y3 + 25*fs_y4))
xm += h * (dxm_dt + (h/192)*(23*fm_x1 + 75*fm_x2 - 27*fm_x3 + 25*fm_x4))
ym += h * (dym_dt + (h/192)*(23*fm_y1 + 75*fm_y2 - 27*fm_y3 + 25*fm_y4))
dxs_dt += h/192 * (23*fs_x1 + 125*fs_x2 - 81*fs_x3 + 125*fs_x4)
dys_dt += h/192 * (23*fs_y1 + 125*fs_y2 - 81*fs_y3 + 125*fs_y4)
dxm_dt += h/192 * (23*fm_x1 + 125*fm_x2 - 81*fm_x3 + 125*fm_x4)
dym_dt += h/192 * (23*fm_y1 + 125*fm_y2 - 81*fm_y3 + 125*fm_y4)
# 接線方向の速度
vs = np.sqrt( dxs_dt**2 + dys_dt**2 )
vm = np.sqrt( dxm_dt**2 + dym_dt**2 )
xs_list.append(xs)
ys_list.append(ys)
xm_list.append(xm)
ym_list.append(ym)
plt.gca().set_aspect('equal')
plt.xlim(-6* 10**5, 1 * 10**5)
plt.ylim(-3 * 10**5, 3 * 10**5)
plt.plot(0, 0, marker='o', color='blue') # 地球
plt.plot(xs_list, ys_list, color='red') # 人工衛星(軌道線)
plt.plot(xm_list, ym_list, color='green') # 月(軌道線)
plt.plot(xs_list[-1], ys_list[-1], marker='.', color='red') # 人工衛星(本体)
plt.plot(xm_list[-1], ym_list[-1], marker='.', color='green') # 月(本体)
plt.pause(0.01)
plt.cla()
print("{0:4d}| 衛星:{1:10.2f}[km/day], 月:{2:.2f}[km/day]".format(i, vs, vm))
上のプログラムを実行すると、人工衛星と月が近づいていってスイングバイをする様子を見ることが出来ます。
スイングバイを行うことで確かに加速していることが確認できますね。人工衛星が次第に減速していくのは、地球の重力に引っ張られているためでしょう。
【参考文献】
- 長沢工・桧山澄子,パソコンで見る天体の動き,株式会社 地人書館,1992年9月20日