はじめに
以前の記事[1]では、相補フィルタに比べて外乱に強い姿勢推定フィルタ(以降、OmegaFFと表記)を提案しました。ただし、そこでいう外乱とは振動や衝撃、電気的なノイズなどによって一時的に計測値を乱すようなものを指しており、計測値にオフセットが生じるような外乱は想定していませんでした。
この”計測値にオフセットが生じるような外乱”ですが、例えば自動車の場合には加減速を行ったりカーブを走行した際に車体の運動によって加速度が生じるため、姿勢推定フィルタからすれば加速度計測値にオフセットが生じているように見え、これを”動加速度”や”動的加速度”と呼びます[2]。
本記事では文献[4]を参考にして、動加速度外乱が加わった場合でも姿勢推定値が悪化しないようにOmegaFFの拡張を行います。
地磁気の場合にもセンサ近傍の配線に電流が流れることでオフセットが生じますが、伏角があったりセンサのオフセットが元々大きかったりと、加速度に比べて扱いが少し厄介なので今回は扱いません。
動加速度外乱の検知・対処
そもそもどうやって対処するか
動加速度外乱によって姿勢推定誤差が増加しないようにするには、実際のところどのように対処すればよいのでしょうか。この問題について、少し考えてみると以下の二つの方法が思い浮かびます。
- 動加速度を推定して加速度計測値から引くことで、重力加速度ベクトルだけ取り出す。
- 動加速度が加わったことを検知したら、加速度による補正を軽減ないしは停止する。
上記二つの方法のうち、動加速度を推定する方法は文献[3]で、補正を軽減・停止する方法は文献[4]で述べられています。
性能の良し悪しは使用状況や設計によると思いますが、動加速度を推定する方法では条件設定を適切に行わないと「動加速度を推定するためには姿勢推定値が必要だけど、姿勢推定のためには動加速度の推定値が必要で…」という循環参照のような状態に陥ってしまいます。
その点でいうと、補正を停止する方法は外乱を検知したら単純に補正を止めるだけで良いのですから非常にシンプルです。ただし、外乱の判定方法や閾値を適切に設定しないと、いつから補正を再開していいかわからないという状況に陥ることがあります。
これらを踏まえると、OmegaFFは角速度バイアスの推定まで行っており、これが正しく推定できていれば角速度を積分するだけで暫くは正しい姿勢変化を計算できるわけですから、外乱を検知したら補正を止めてしまうのが得策と考えられます。
外乱判定
外乱が加わったかどうかを判定するための式として、文献[4]中で以下の二つの式が紹介・提案されています(文献中の表記とは少し異なります)。
$[ E1(\mathbf{a}_\mathrm{b}, \mathbf{a}_\mathrm{r}) = \frac{ \mathrm{abs}( \| \mathbf{a}_\mathrm{b} \| – \| \mathbf{a}_\mathrm{r} \| )}{\| \mathbf{a}_\mathrm{r} \|} $] $[ E2(\mathbf{a}_\mathrm{b}, \mathbf{a}_\mathrm{r}, \tilde q) = \frac{ \| \mathbf{a}_\mathrm{b} – \tilde q^* \mathbf{a}_\mathrm{r} \tilde q \|}{ \| \mathbf{a}_\mathrm{r} \|} $]ここで、 $( \mathbf{a}_\mathrm{b} $) は機体座標系上における加速度計測値、 $( \mathbf{a}_\mathrm{r} $) は基準座標系上における加速度ベクトル(ENU座標系なら[0, 0, 9.80665])、$( \tilde q $)は四元数表現の姿勢推定値を表します。
外乱への対処
上述した外乱判定式の値により、外乱を”弱い外乱”と”強い外乱”に分けて処理を行います。
弱い外乱の場合には補正を完全に止めることはせず、補正角速度の計算パラメータ$( \alpha $)の値を倍にすることで外乱の影響が推定値に強く反映されないようにします。
強い外乱の場合には、 $( \tilde q_\mathrm{gm} $) の計算に用いる加速度ベクトルを $( \mathbf{a}_\mathrm{b} $) ではなく $( \tilde q^* \mathbf{a}_\mathrm{r} \tilde q $) とすることで加速度による補正を停止します。この場合も角速度バイアスの値は保持されるので、暫くは角速度の積分だけで姿勢変化を計算することができます。
また、文献[4]中において
また,外乱の影響が検知された状況から検知されない状況へと推移する場合にはヒステリシス処理を設けている.
文献[4](5.3 外乱検知の評価)
という記述があったので本記事の実装でもヒステリシス処理を設けました。文献中では実際にどの程度のヒステリシス領域を設けたかについては述べられていなかったので、本記事では閾値に対して20%のヒステリシス領域を設けています。
弱い外乱として判定する閾値を $( \varepsilon_1 $) 、強い外乱の閾値を $( \varepsilon_2 $) とすると、ヒステリシス処理を含む二段階の外乱判定は以下のようになります。
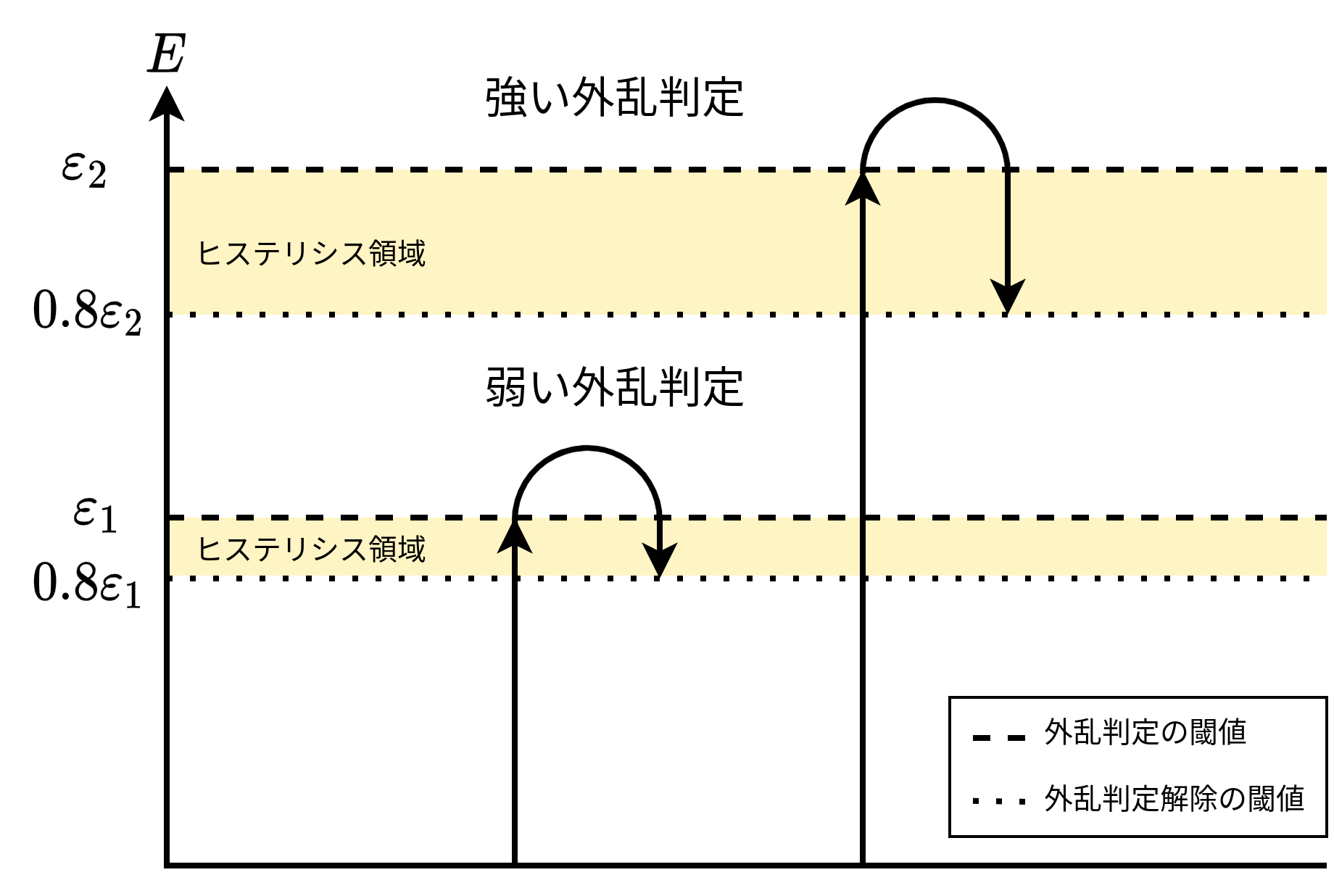
アルゴリズム全体をブロック線図にまとめると以下のようになります。
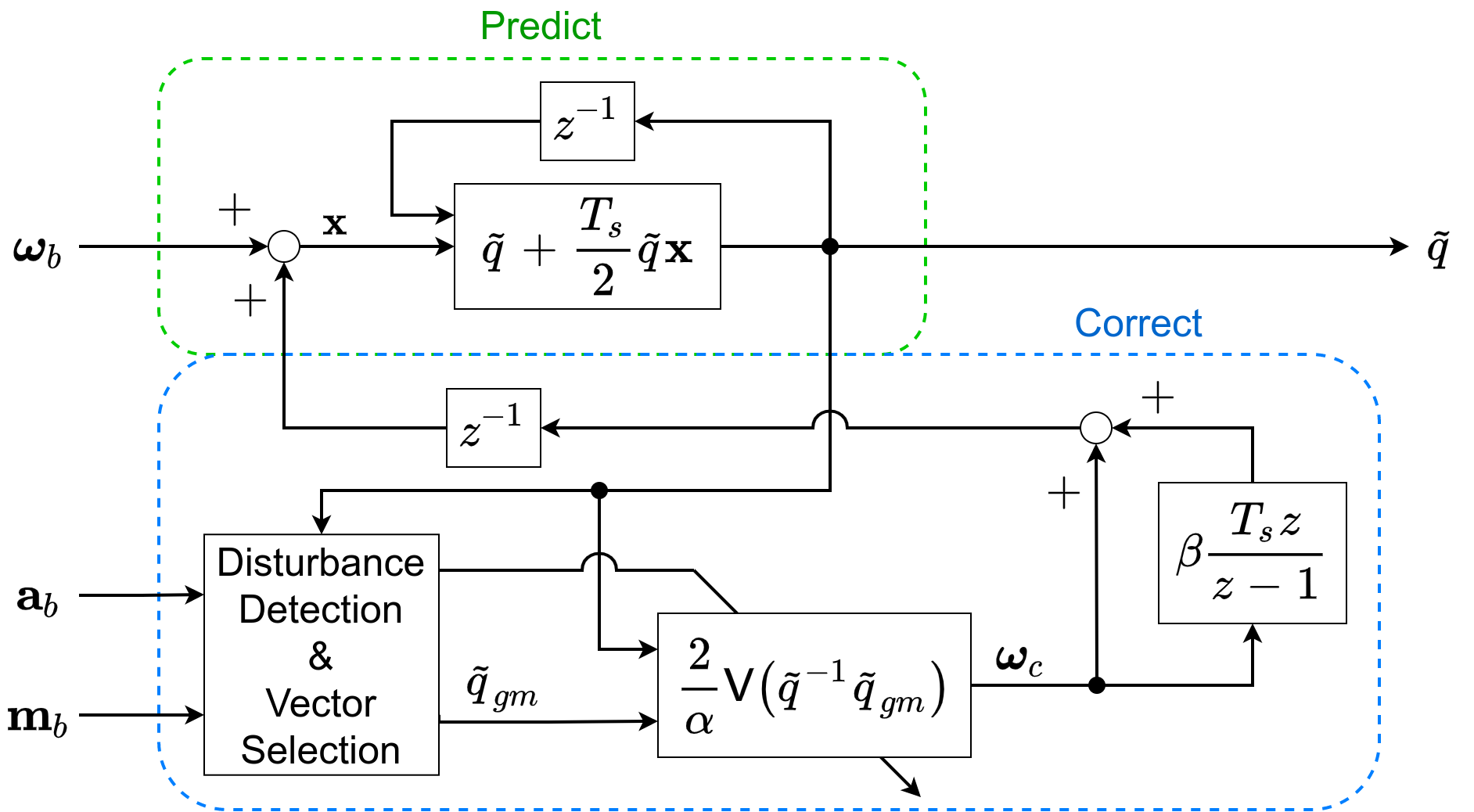
外乱検知を行うようにしたのでLPFは無くしました。そのため、設計パラメータとしてはOmegaFFに元々あった$( \alpha, \beta $)と外乱判定の閾値 $( \varepsilon_1, \varepsilon_2 $) の計4つとなります。
シミュレーション
手元の機材では動加速度外乱を印加する実験を行うことができないので、シミュレーションにて挙動を確認します。
今回のシミュレーションでは、動加速度外乱を考慮していない通常のOmegaFF(Normalと表記)と、外乱判定式にE1とE2を用いた場合の比較を行います。
全てのシミュレーションに共通する条件は以下のとおりです。
- サンプリング周期:0.02 s
- 角速度計測値に加わるノイズ分散:0.0001
- 加速度 〃 :0.01
- 地磁気 〃 :0.01
- 角速度バイアス[x, y, z]:[-0.02, 0.01, 0.05] rad/s
- LPFのカットオフ周波数:10 Hz
- $( \alpha$) = 1.0
- $( \beta$) = 0.2
- $( \varepsilon_1 $) = 0.04
- $( \varepsilon_2 $) = 0.08
一定の加速度外乱が加わる場合
まず、推定開始後10秒から20秒までの範囲において、 $( 3 \; \mathrm{m/s^2} $) の加速度外乱が計測値に加わる場合のシミュレーションを行います。
$( 3 \; \mathrm{m/s^2} $) というと、自動車で少し強めのブレーキを踏んだ場合と同程度です。これが10秒間印加されるので条件としてはかなり厳しくなっています。
この場合のシミュレーション結果を以下に示します。
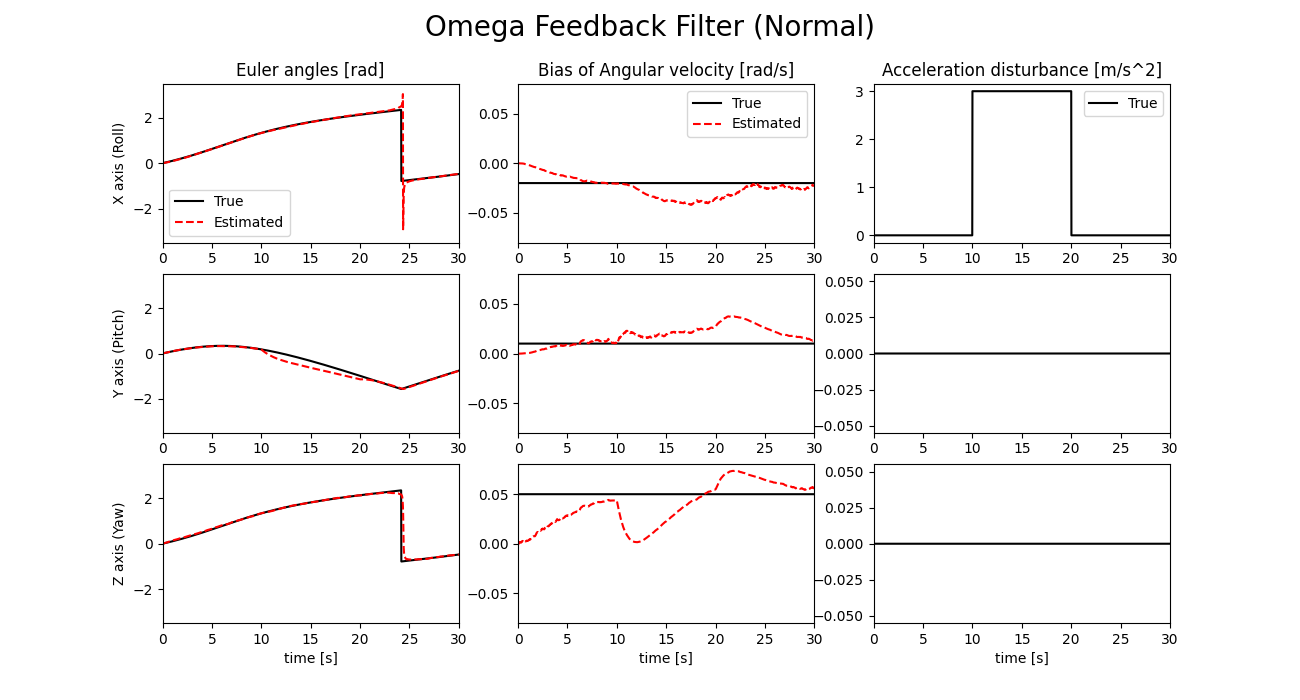
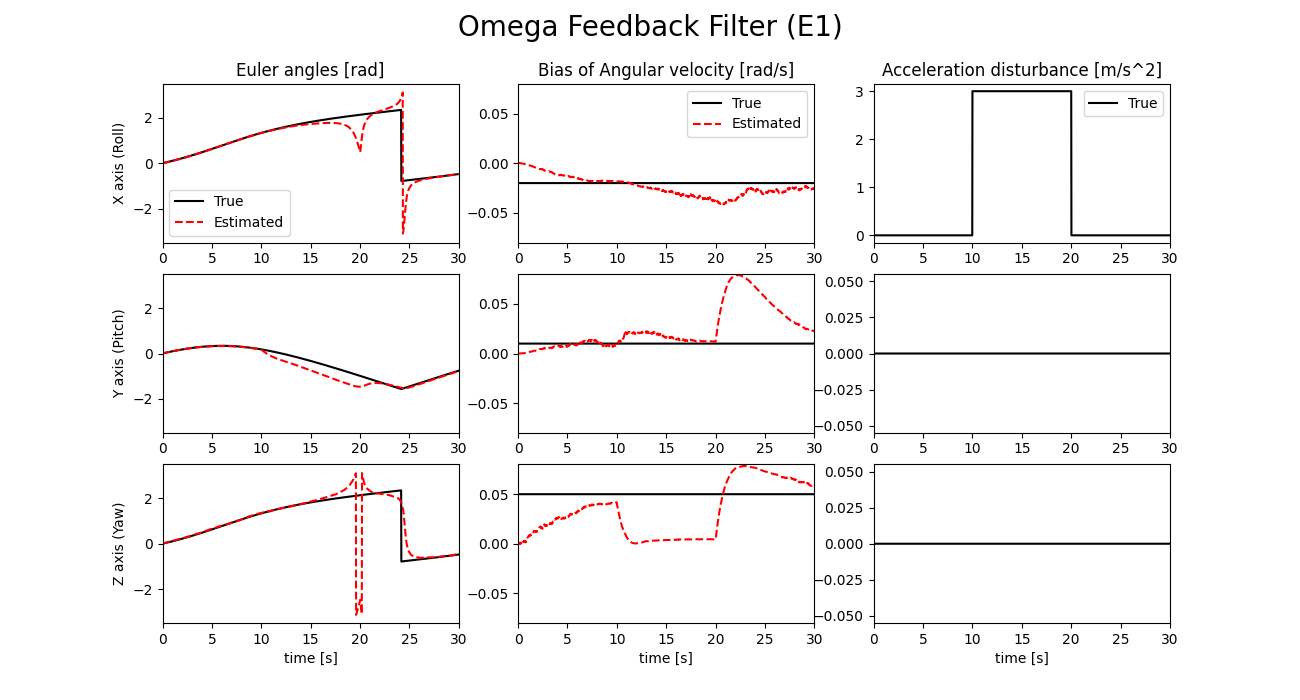
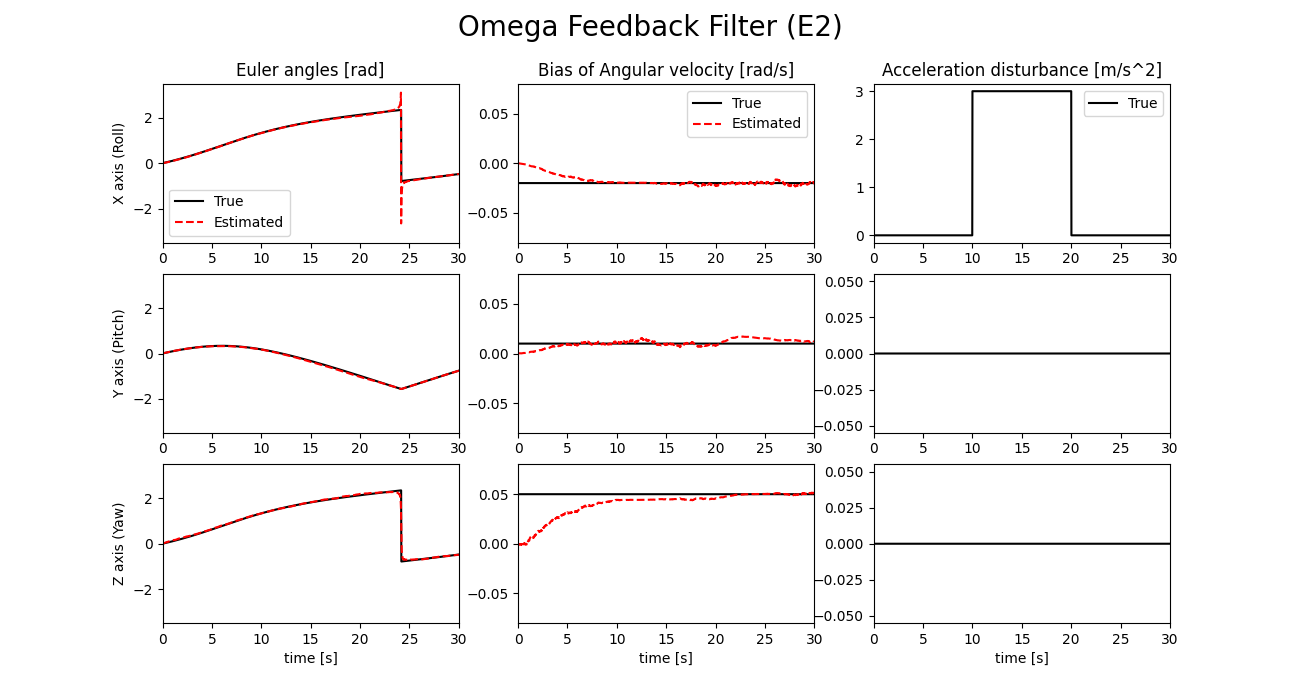
また、このシミュレーション中における外乱判定式E1とE2の値を以下に示します。
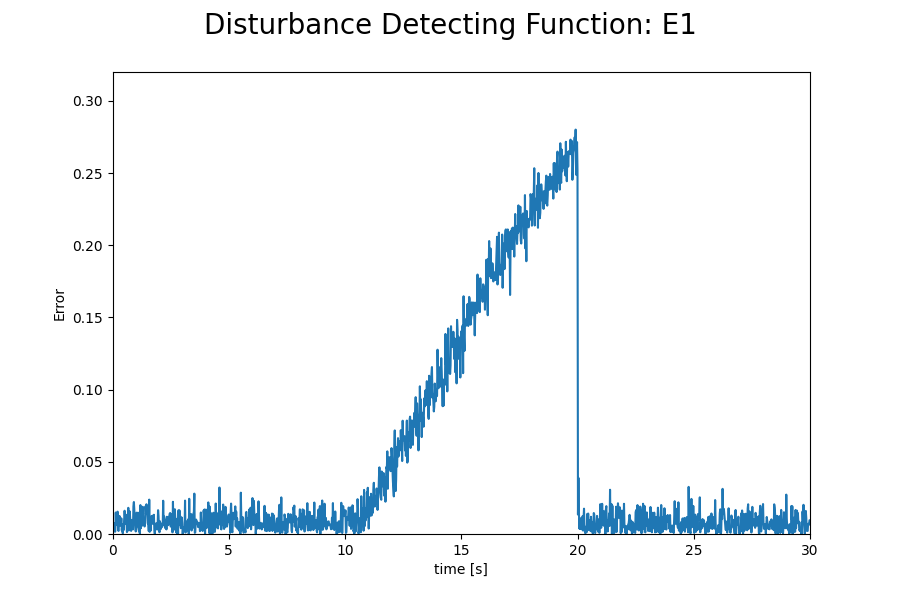
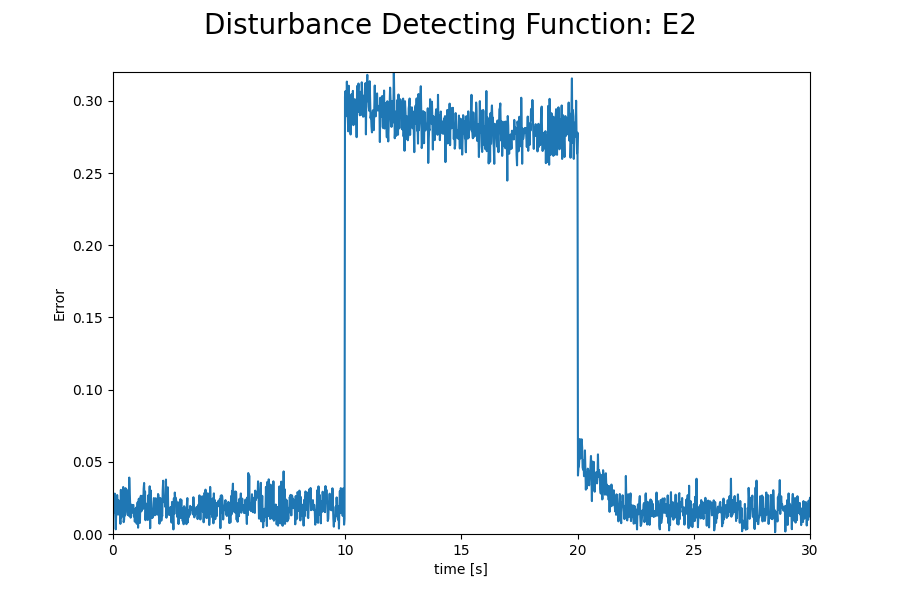
シミュレーション結果を見ると、E2ではほとんど姿勢推定誤差が生じていない一方で、NormalとE1では大きな誤差が生じていることが確認できます。NormalでPitch角に誤差が生じるのは予想通りというか、そういうアルゴリズムなので良いのですが、E1は外乱対策をしていないNormalよりも誤差が大きくなってしまっています。
ここで判定式E1の値を見てみると、外乱が加わってから4秒ほど経過するまでは$( \varepsilon_2 $)を超えておらず、補正が継続されていることがわかります。補正が継続されている間に角速度バイアスの推定値が外乱の影響を受けたため、最終的にNormalよりも姿勢推定誤差が大きくなってしまったと考えられます。
このように、判定式によって外乱が加わった際の挙動は大きく変化します。文献[4]中でも言及されていますが、E2では誤差成分を直接評価しているためE1に比べて感度が高く、上記のシミュレーションでは非常に良い結果を示しました。
初期姿勢に誤差がある場合
先のシミュレーションで非常に良い結果を出した判定式E2ですが、良いところがあれば悪いところもあります。
式を見て気づいた方もいるかもしれませんが、E2では外乱が加わった状態と姿勢誤差を判別することができません。そのため、姿勢推定開始時など推定誤差が大きい場合には真値に収束しなくなってしまいます。
初期姿勢に大きな誤差がある場合のシミュレーション結果を以下に示します。
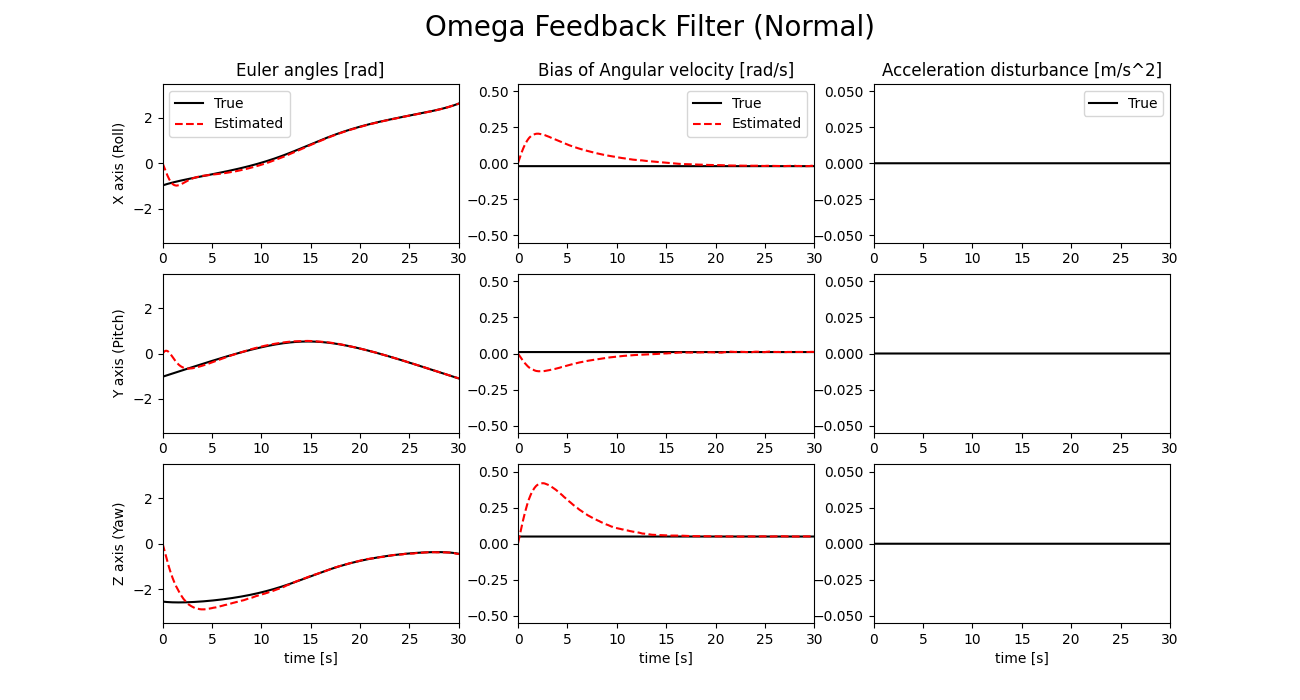
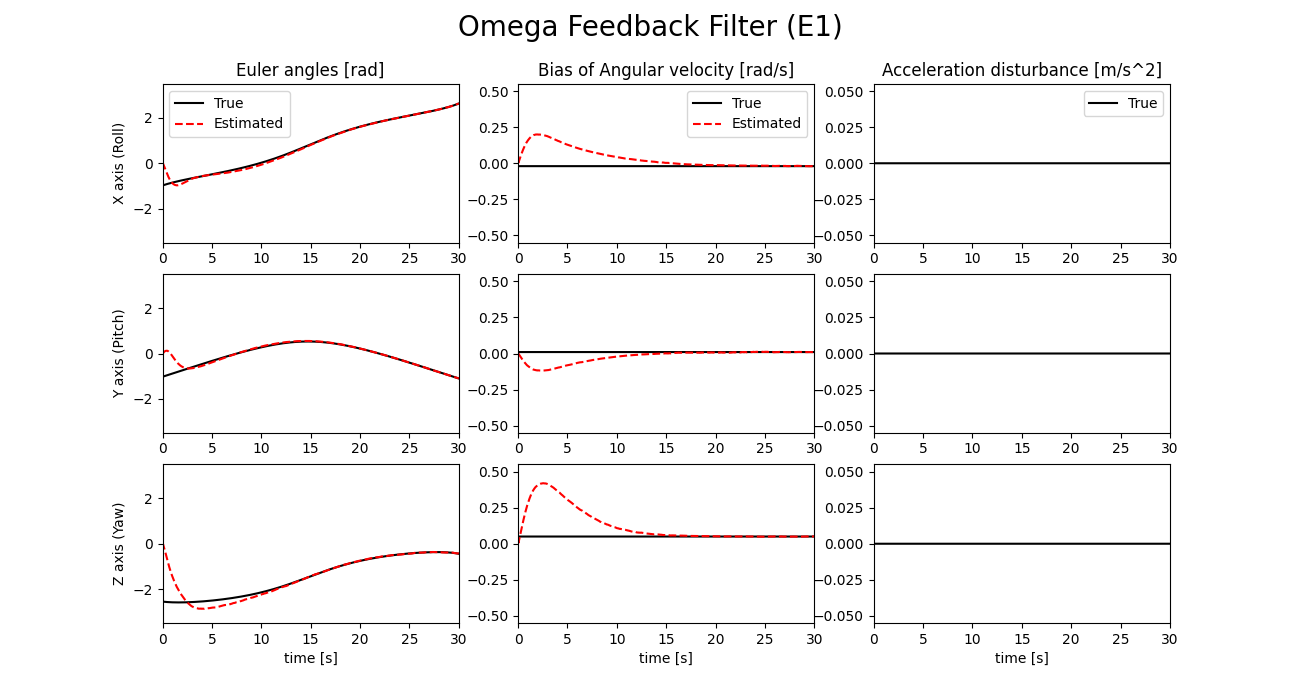
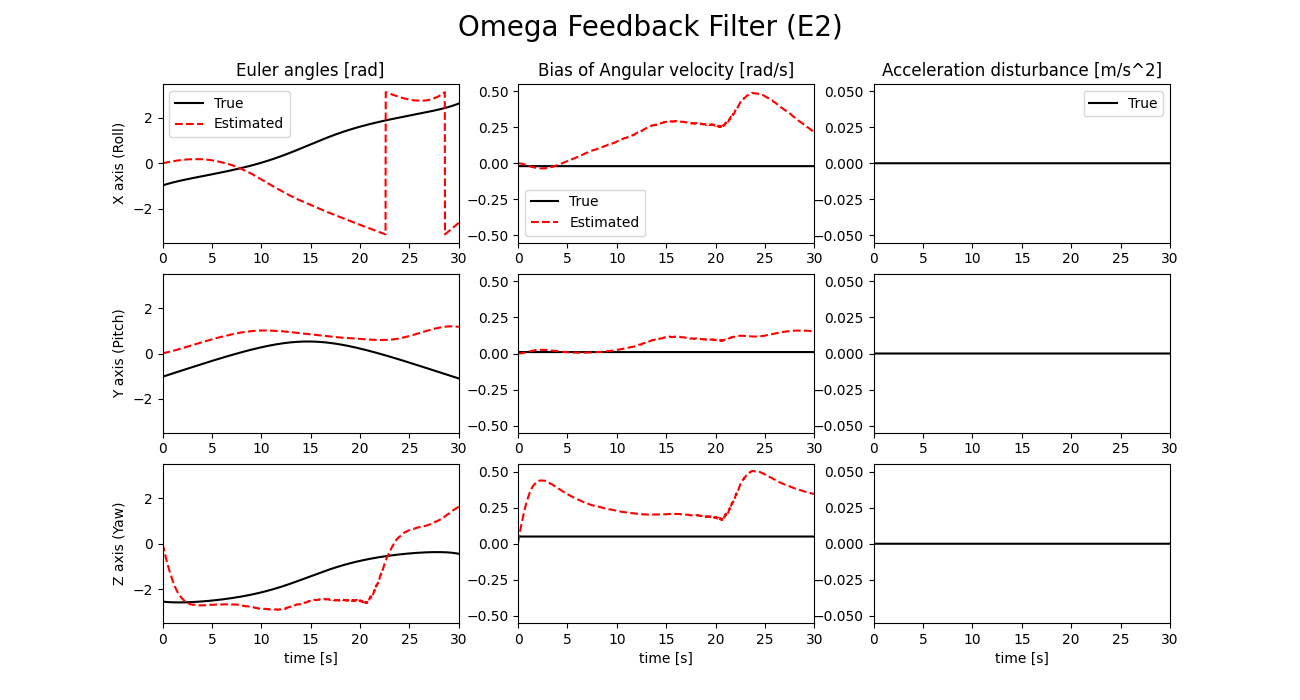
外乱判定式E1とE2の値を以下に示します。
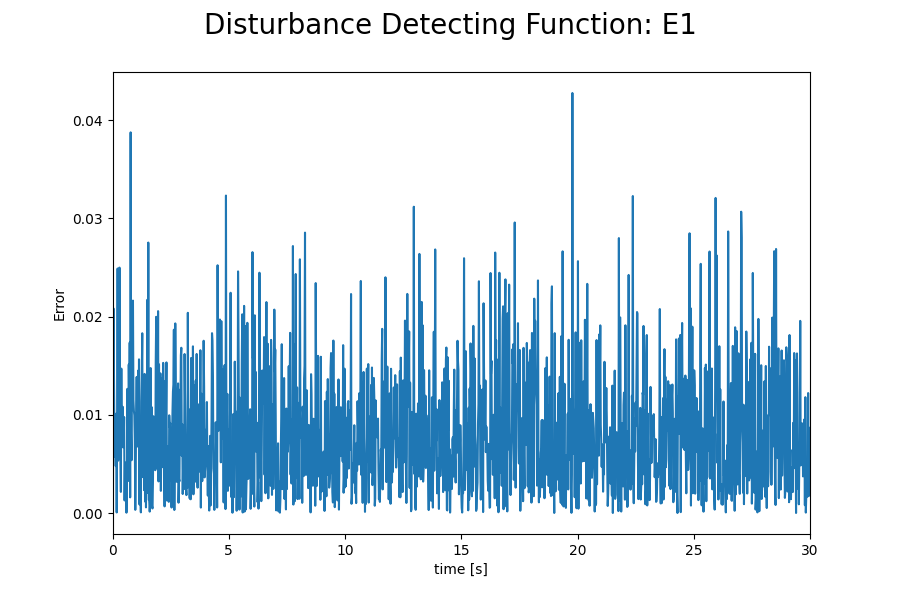
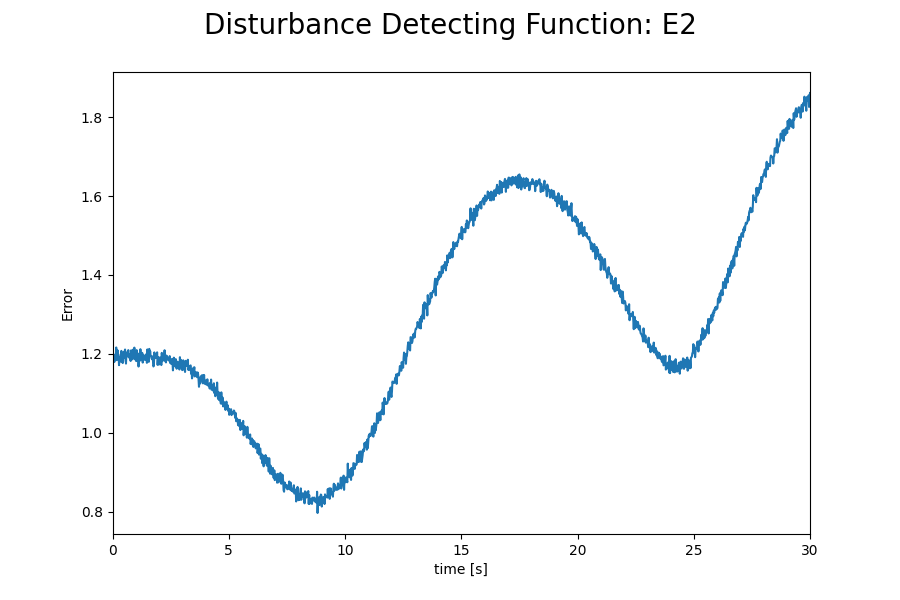
上図より、判定式E2を用いた場合には初期姿勢の誤差が大きいと真値に収束しないことがわかります。
ただし、このケースでは加速度と地磁気から求めた$( \tilde q_\mathrm{gm} $)を初期姿勢とすることで対処できます。一方で、強い外乱を検知して長期間補正が止まってしまうような状況では、次第に誤差が蓄積して正常な状態に復帰できなくなることが想定されます。
劣悪な外乱が長時間加わる場合
姿勢誤差が大きくなるように、外乱判定の閾値近傍をふらつくような外乱を長時間加えてみましょう。シミュレーション結果を以下に示します。
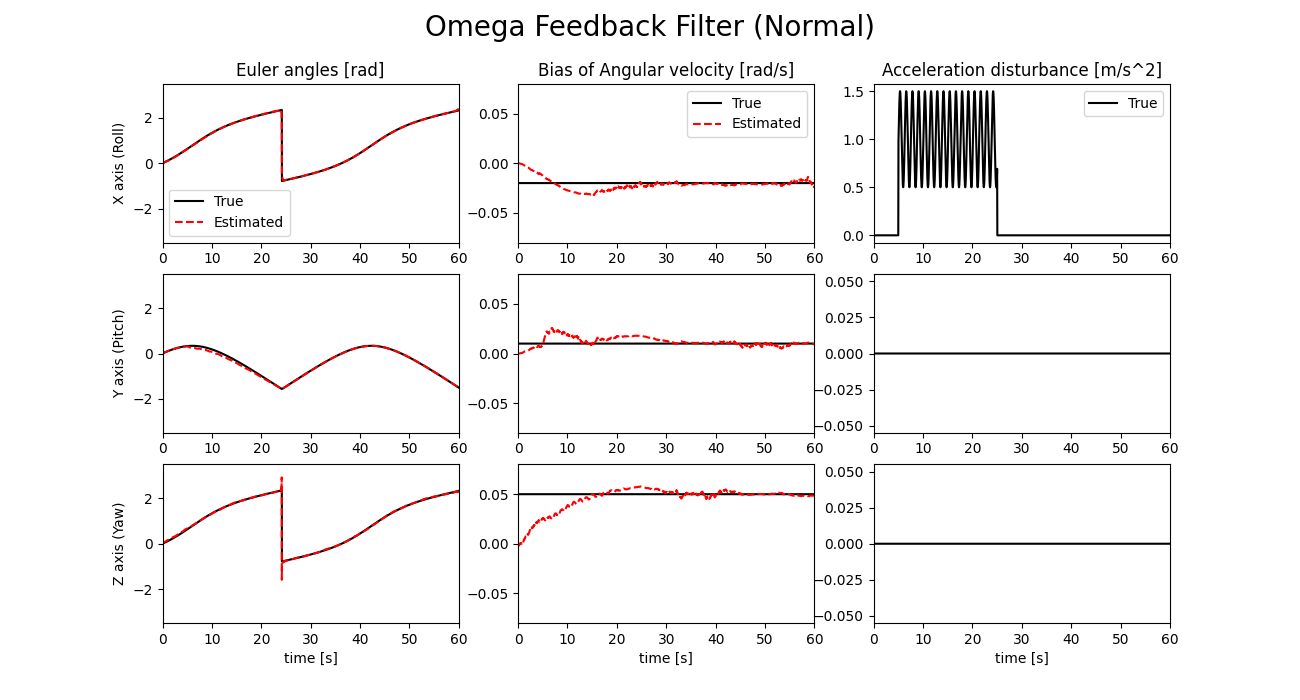
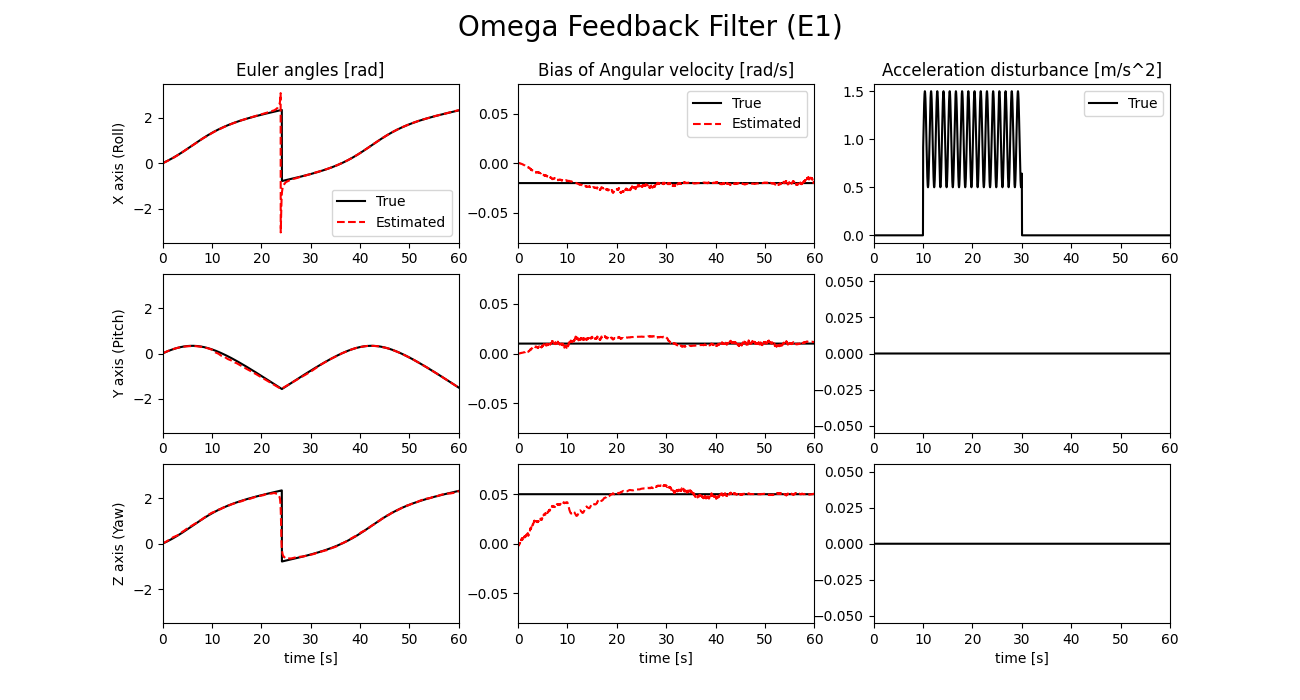
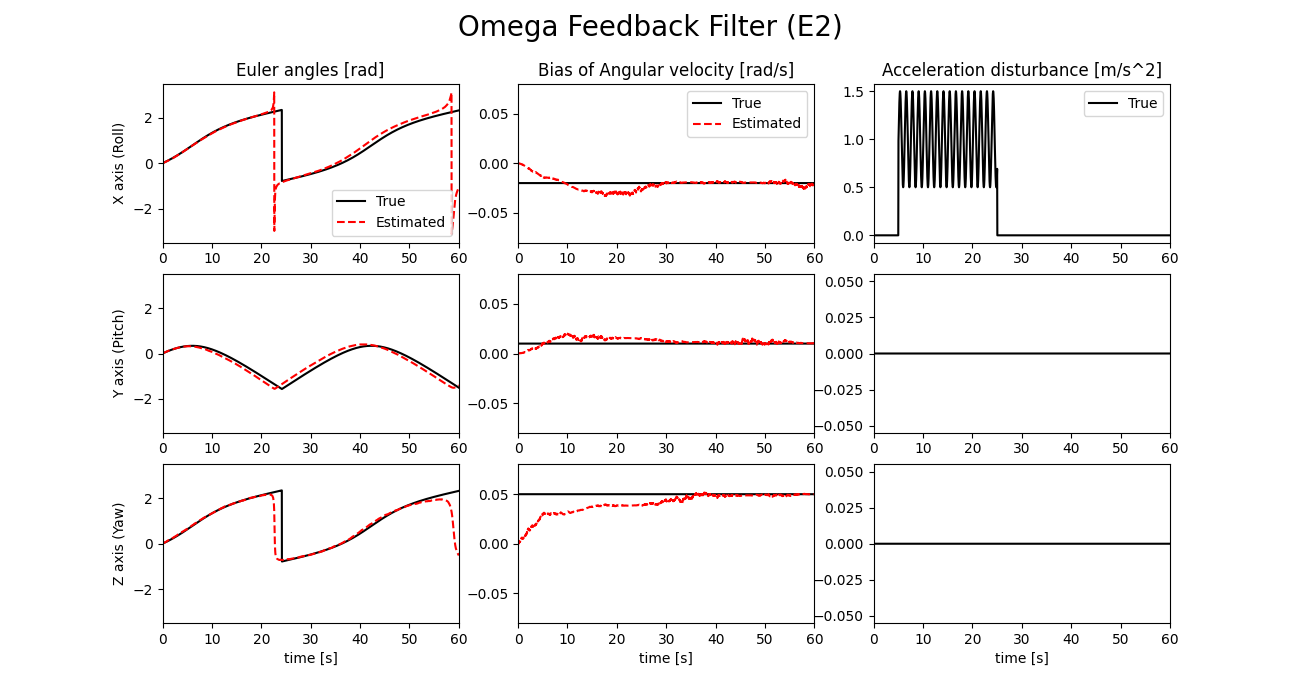
外乱判定式E1とE2の値を以下に示します。
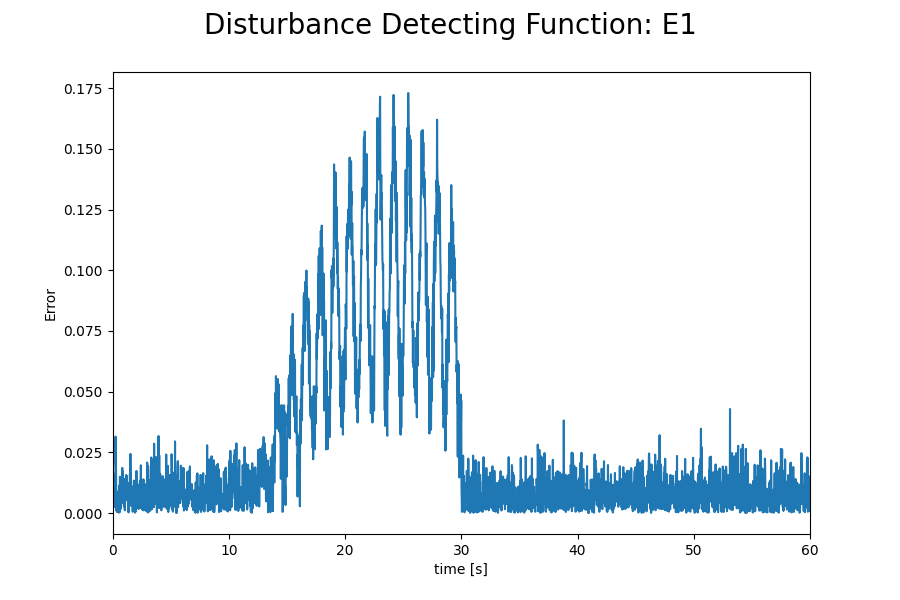
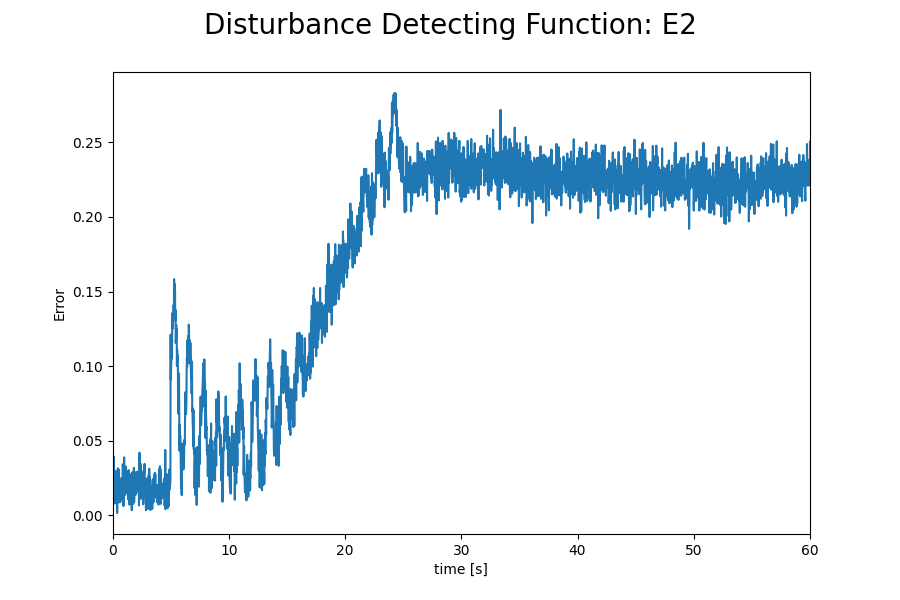
判定式E2を使用したフィルタでは外乱が印加されなくなった後も判定式の値が閾値を超えており、補正が止まったままであることがわかります。
使用したプログラム:https://github.com/HamaguRe/space-denpa_omega-ff_dynamic-acc
実験
一定の加速度外乱を加えることはできませんが、OmegaFFから構造を変更したので動作確認という意味で実験を行いました。
地磁気センサの較正を行っていないので実験動画の中でヨー角がかなり大きくドリフトする場面が見られますが、加速度外乱除去の検証には影響しないことを予め断っておきます。
フィルタの設計パラメータとサンプリング周期はシミュレーションの場合と同じです。また、3つのフィルタは全て同じ計測値を使用してマイコン(STM32F303K8T6)上で計算を行っています。
まず、シミュレーションと同条件のもとNormal, E1, E2で比較実験を行いました。
【 Normal, E1, E2での比較実験映像.mp4 】
いざ実験を行ってみると、予想以上にE2の外乱判定がシビアですぐに補正が止まってしまうことがわかりました。実際のセンサにはオフセットやスケールファクタ誤差が存在すること、回転中心が必ずしもセンサと一致しないため長時間に渡って外乱が加わっているような状態となっていることが原因として考えられます。
また、動画の撮影開始時はセンサを静置していますが、この時点で既に判定式E1とE2の値が0.04程度となっており弱い外乱として判定されていることがわかります。アルゴリズム内では$( \mathbf{a}_\mathrm{r} $)のノルムが標準重力(9.80665)となるようにしていますが、実際に計測される値はセンサのオフセットや地理的な要因により標準重力とは異なるため、その分のズレが判定式の値に現れていると考えられます。
そこで、E2を変更して新たに判定式E3を考案しました。
$[ E3(\mathbf{a}_\mathrm{b}, \mathbf{a}_\mathrm{r}, \tilde q) = \left\Vert \frac{\mathbf{a}_\mathrm{b}}{\| \mathbf{a}_\mathrm{b} \|} – \tilde q^* \frac{\mathbf{a}_\mathrm{r}}{\| \mathbf{a}_\mathrm{r} \|} \tilde q \; \right\Vert $]この式では単に $( \mathbf{a}_\mathrm{b} $) と $( \mathbf{a}_\mathrm{r} $) の向きだけを比較するため、上述した計測誤差や、姿勢推定に影響を及ぼさない外乱(例えば、自動車が一定速度で走行している際に加わる鉛直方向の振動など)に反応せずに済むという利点があります。 $( \| \mathbf{a}_\mathrm{b} \| =0 $) となる可能性があるのでゼロ除算が発生しないように注意する必要はありますが、判定式E2よりも実環境向けだと思います。
E3の動作検証を行うため、パラメータは最初の動画と同じにしてNormal, E2, E3で比較実験を行いました。
【 Normal, E2, E3での比較実験動画.mp4 】
狙い通り、静置状態における判定式の値が2桁小さくなっています。しかし、相変わらずすぐに収束しなくなってしまいました。
思い切って外乱判定の閾値を大きくしてみましょう。理論上の推定誤差は大きくなりますが、収束しなくなってしまっては元も子もないのでそこは目を瞑ります。
外乱判定の閾値を$( \varepsilon_1=0.1, \varepsilon_2=0.5 $)に変更して、Normal, E2, E3で比較実験を行った動画を以下に示します。
【 Normal, E2, E3での比較実験動画.mp4(閾値を変更) 】
これでようやく収束性を維持できるようになりました。しかし、アルゴリズムとして収束性が保証されているわけでは無いという点には注意が必要です。
おわりに
本記事では、動加速度外乱に対処するためにOmegaFFの拡張を行い、シミュレーションを通して外乱判定式の違いによる姿勢推定精度の比較を行いました。また、実験を通してシミュレーションの理想的な条件では生じない問題があることを確認し、それに対処する方法を示しました。
さて、結局どの判定式を使えば良いのかと聞かれると、これはなかなか難しいところです。
E2(ないしはE3)は外乱に対する感度が高く、理想的な状況であれば最初のシミュレーション結果で示したようにとても良い結果を出してくれます。しかし、外乱の加わり方によっては補正が止まったままになり、推定精度どころでは無くなってしまうことがあります。
一方、シミュレーションではあまり良い印象のなかったE1ですが、実験を行っている際には”ちゃんと収束してくれる”というだけでかなり安心感がありました。E2に比べて感度が低いという問題はあるものの、瞬間的に大きな加速度外乱が加わる状況ではE1を使うのも悪くないと思います。
もしくは、とりあえず安定して姿勢計測したいという用途では外乱検知を行わない素のOmegaFFを使用するという選択肢もあります。動加速度外乱の印加時間が短時間かつ$( \alpha $)が大きければそこまで大きな姿勢誤差は生じませんから、最初から動加速度外乱まで考慮して複雑なシステムを組むよりは、まずは構成のシンプルなOmegaFFで様子を見たほうが良いと思います。
上記を踏まえた上で本記事の結論を出すとすれば、「高い姿勢推定精度を求めるなら、しっかりとセンサの較正を行った上でE2かE3を使うべき。安定性を重視するなら、E1か素のOmegaFFを使ったほうが良い。」となります。
参考文献
- 宇宙電波実験室, “角速度の形でフィードバックを行う姿勢推定フィルタ”, (参照2022-03-26).
- 鈴木 智, 田原 誠, 中澤 大輔, 野波 健蔵, “動加速度環境下における姿勢推定アルゴリズムの研究”, 日本ロボット学会誌, Vol. 26, No. 6, 2008.
- 田原 誠, 鈴木 智, 野波 健蔵, ”小型軽量汎用性を特徴とする小型姿勢センサの開発”, 日本機械学会論文集(C編), Vol. 77, No. 781, 2011.
- 大和 秀彰, 古田 貴之, 富山 健, ”外乱に対して頑強で大域的漸近安定なジャイロバイアス誤差の推定・除去による三次元姿勢推定”, 日本機械学会論文集(C編), Vol. 77, No. 776, 2011.