パルス幅一定なら，それっぽいのが出力できます。

リアルタイム描画など，基本的なところは「Matplotlibで正弦波をリアルタイム描画する」の内容と同じです。

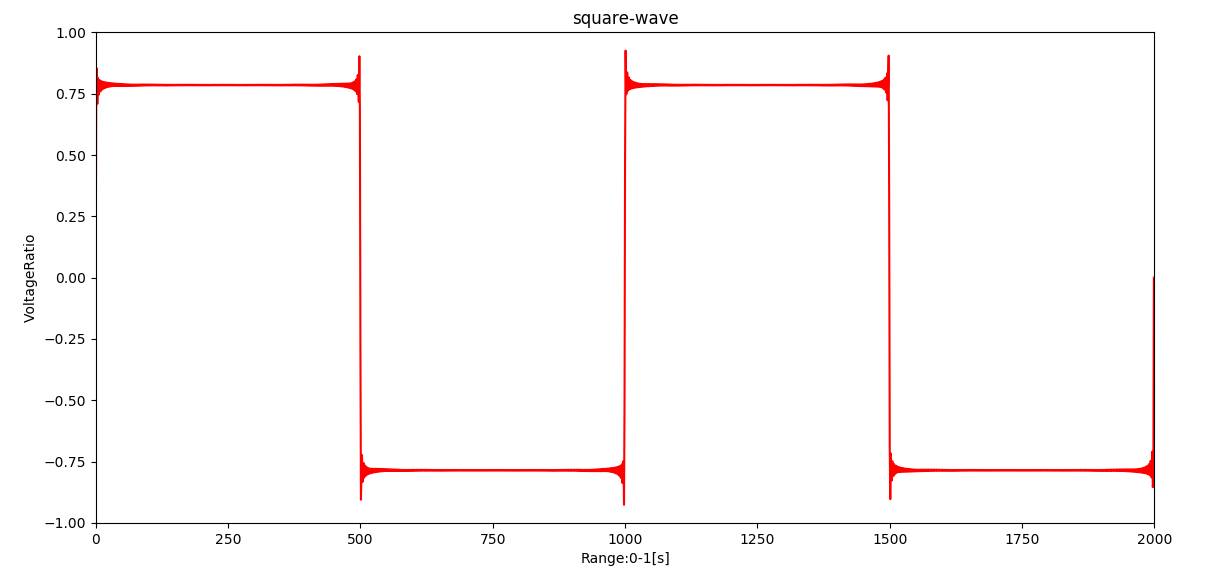
取り敢えずプログラムを…

# Python3
# N=160辺りで落ち着いてくる

import math
import numpy as np
import matplotlib.pyplot as plt

def square(n, f):    # n:重み，f:周波数
    pi = math.pi
    plt.title("square-wave")
    plt.ylabel("VoltageRatio")
    plt.xlabel("Range:0-1[s]")
    x = np.linspace(0, 2*pi, 2000)
    plt.ylim(-1, 1)
    plt.xlim(0, 2000)

    # 初期値
    N = 1
    y = 0
    y1 = 0
    for N in range(1, n):
        # 矩形波を作る式。Σで積んでくと矩形波に近づく。
        y = (1/(2*N-1)) * np.sin((2*N - 1)*x * f)
        y1 += y
        N += 1

    plt.plot(y1, color='red')
    plt.pause(0.1)
    print("周波数:",f ,"[Hz]・", "重み:N=", n)

    plt.cla()

f = float(input("周波数は何[Hz]？")) 
if f > 0 : 
    n = 0
    while n < 200 :
        n += 1 
        square(n, f)
else:
    f = float(input("周波数は何[Hz]？"))

今回は矩形波の生成過程が見たかったので，周波数fではなく重みNを変化させてループさせています。

矩形波を作る式は以下の通り。

Nは重み，fは周波数で，Nを増やすと矩形波に近づいていきます。

おまけ（ってほどでもないか）

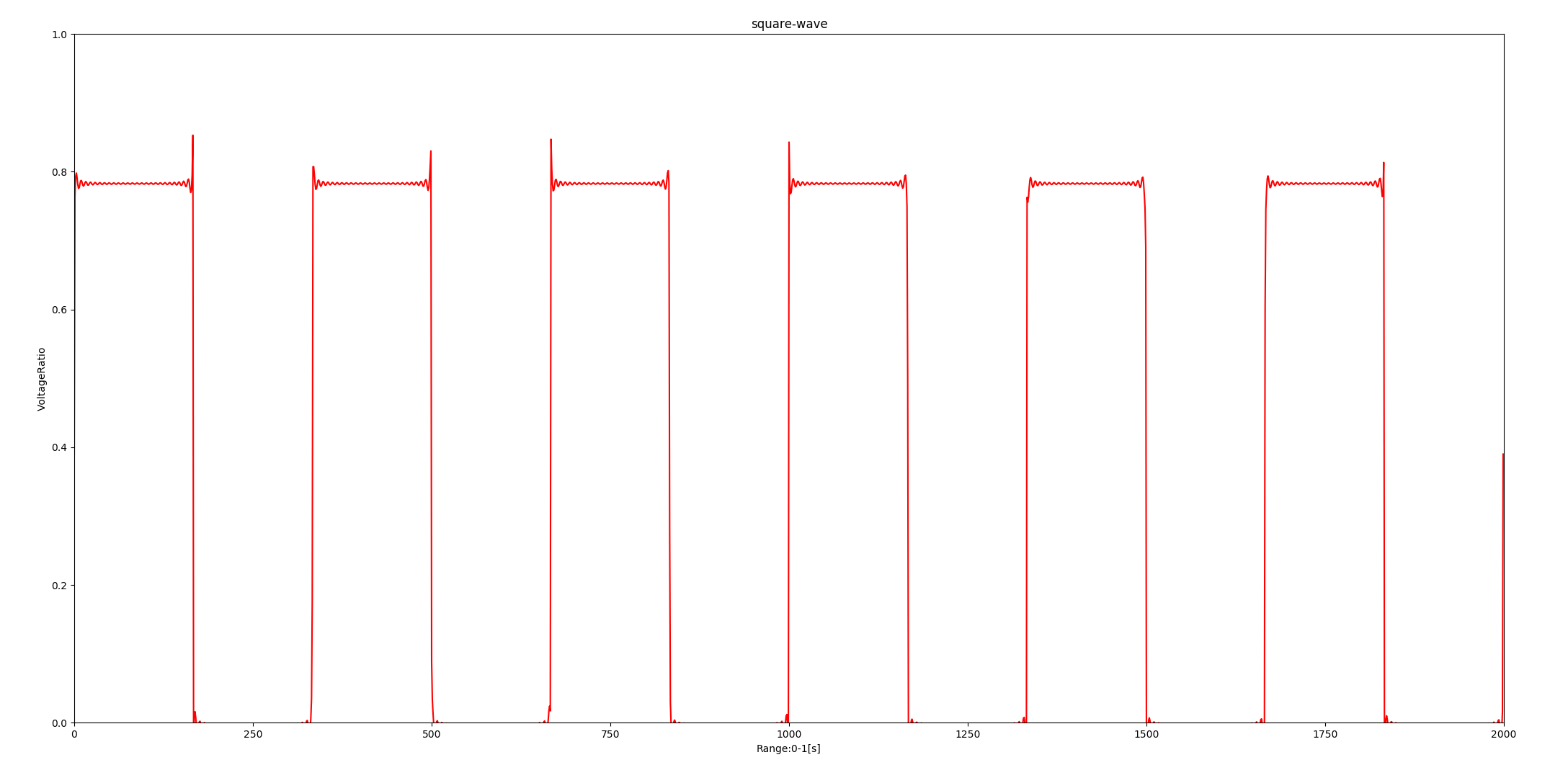
数式を少し弄って y > 0 だけで表示するようにしてみました。

# Python3

import math
import numpy as np
import matplotlib.pyplot as plt

def square(n, f):    # n:重み，f:周波数
    pi = math.pi
    plt.title("square-wave")
    plt.ylabel("VoltageRatio")
    plt.xlabel("Range:0-1[s]")
    x = np.linspace(0, 2*pi, 2000)
    plt.ylim(0, 1)
    plt.xlim(0, 2000)

    # 初期値
    N = 1
    y = 0
    y1 = 0
    for N in range(1, n):
        # 矩形波を作る式。Σで積んでくと矩形波に近づく。
        y = (1/(2*N-1)) * np.sin((2*N - 1)*x * f)
        y1 += y
        N += 1

    bias = 0.39
    plt.plot((y1 * 0.5)+bias, color='red')
    plt.pause(0.1)
    print("周波数:",f ,"[Hz]・", "重み:N=", n)

    plt.cla()

f = float(input("周波数は何[Hz]？"))
if f > 0 :
    n = 0
    while n < 200 :
        n += 1
        square(n, f)
else:
    f = float(input("周波数は何[Hz]？"))