本記事の表題となっている“Versor求解アルゴリズム”とは、3次元ベクトル\( \boldsymbol{a} \)と\( \boldsymbol{b} \)が与えられた場合に
$$\boldsymbol{b} = \tilde{q} \boldsymbol{a} \tilde{q}^{-1} \tag{1}$$
を満たす\( \tilde{q} \)を求めるアルゴリズムのことを指します。上式を満たす\( \tilde{q} \)は複数存在するため求め方も複数存在し、上手く求めないと特異点が生じてしまいます。特異点は無いに越したことはないので、本記事では特異点を持たない求解アルゴリズムを示します。
記事中に数式を書くと式参照がやりにくいので、内容はPDFにまとめました。以下のリンクからご覧ください。
上記の資料を読むにあたっては以前書いた四元数まとめ資料が参考になるかと思います。
また、5章で軽く触れている姿勢計算に関しては以下の記事に詳しく書いています。
『加速度・地磁気センサの値から姿勢（四元数表現）を求める』（宇宙電波実験室）
【おまけ】数値例
上記PDF中で示した二つのアルゴリズムをプログラムに実装して計算結果を比較します。ただし、筆者は数値計算の専門家ではないので、雑に比較してもこんなに差が出るんだなーくらいの気持ちで見て下さい。
比較方法として、まず基準となる四元数\( \tilde{q}_o \)とベクトル\( \boldsymbol{a} \)を用意してベクトル\( \boldsymbol{b} \)を計算します。
$$\boldsymbol{b} := \tilde{q}_o \boldsymbol{a} \tilde{q}_o^{-1} \tag{2}$$
ここで\( \tilde{q}_o \)は
$$ \tilde{q}_o := \cos \frac{\theta}{2} + \boldsymbol{n} \sin \frac{\theta}{2} \tag{3}$$
とし（ただし\( \boldsymbol{a} \perp \boldsymbol{n} \)かつ\( \| \boldsymbol{n} \| = 1 \) ）、\( \theta \mathrm{[rad]}\)を\( 0 \)〜\( 2 \pi \)の範囲で動かすことで\( \boldsymbol{a} \)と\( \boldsymbol{b} \)の位置関係を調整します。
次に、\( \boldsymbol{a} \)と\( \boldsymbol{b} \)より求解した四元数を\( \tilde{q}_r \)として誤差ベクトルを以下のように定義します。
$$ \boldsymbol{e} := \boldsymbol{b} – \tilde{q}_r \boldsymbol{a} \tilde{q}_r^{-1} \tag{4}$$
上式における\( \tilde{q}_r \)を二つのアルゴリズムでそれぞれ求めることで、計算精度を比較します。なお、今回はアルゴリズムによってどの程度結果が変わるかの比較なので単精度で計算しました。
まず、特異点を持つ従来のアルゴリズムを用いた場合の計算結果を示します。
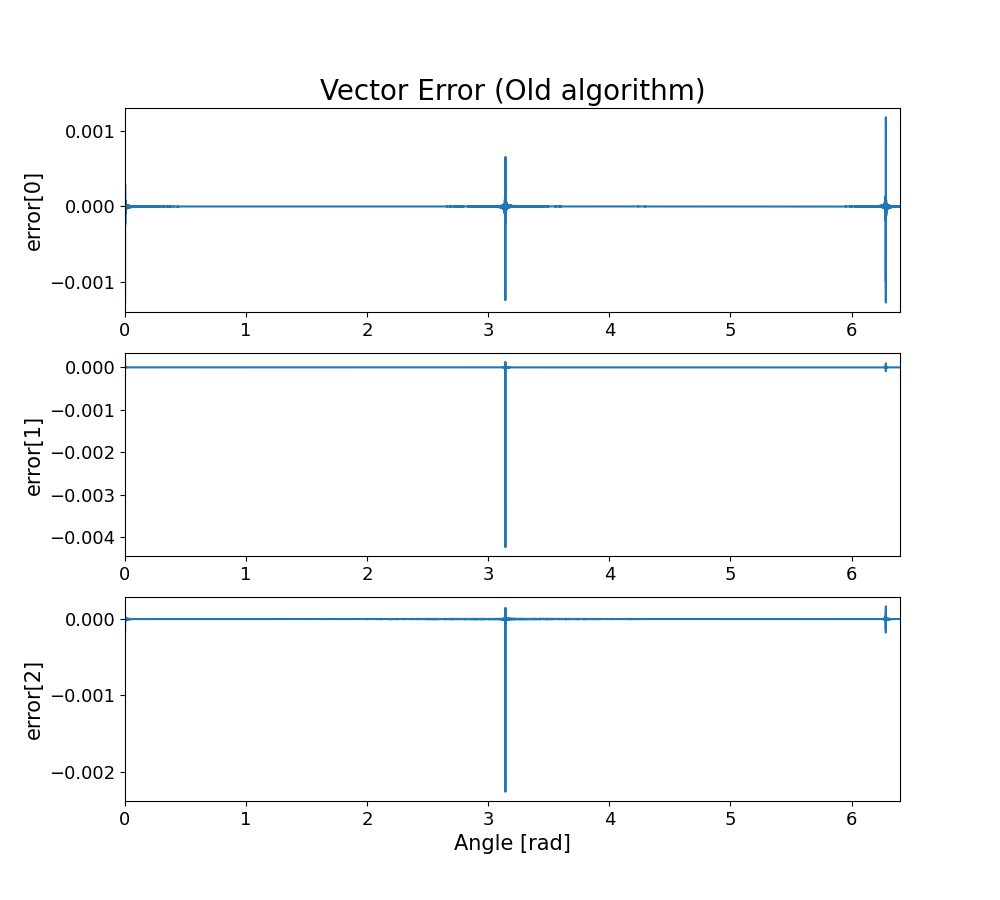
グラフの横軸は式(3)における\( \theta \)となっており、上から順に誤差ベクトル\( \boldsymbol{e} \)の第一・第二・第三要素の値を表しています。
このアルゴリズムは\( \boldsymbol{a} \parallel \boldsymbol{b} \)のときに特異点をとるため、グラフを見ると特異点近傍で誤差が大きくなっていることがわかります。
次に、特異点を持たない新しいアルゴリズムを用いた場合の計算結果を示します。
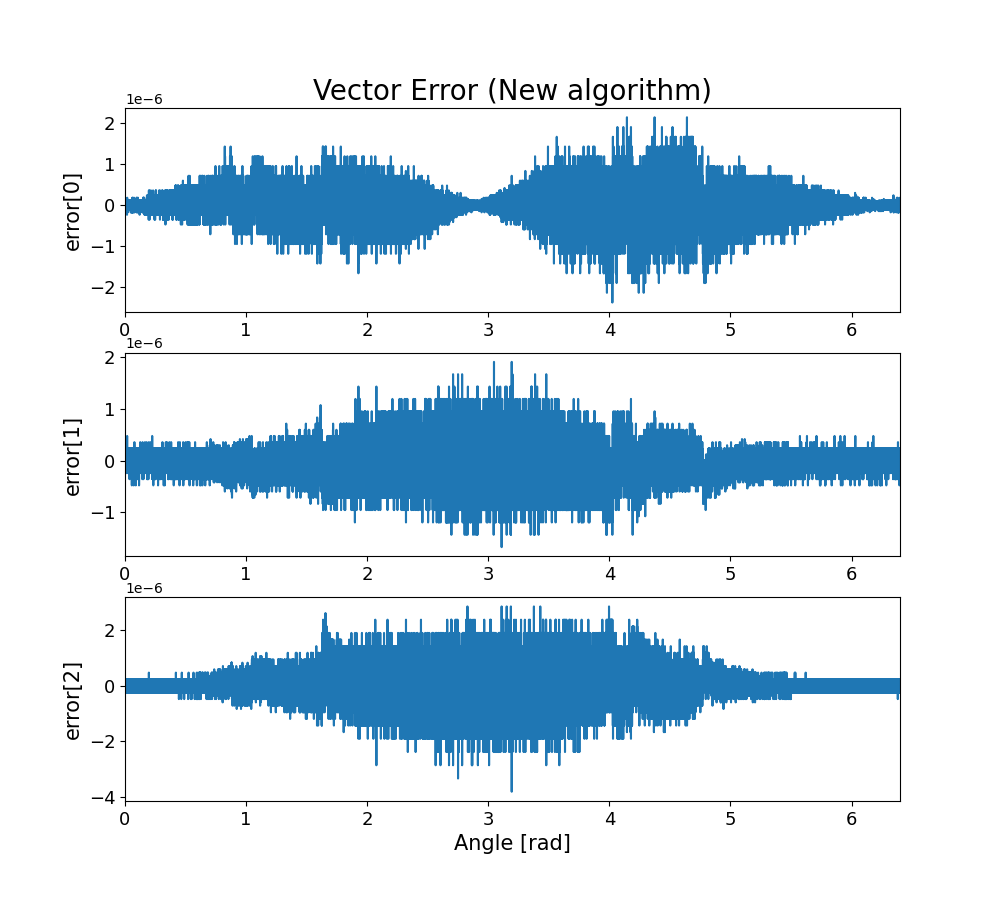
一見先程のグラフよりも汚く見えますが、スケールが\( 10^{-6} \)なので全域で誤差が非常に小さくなっています。今回は単精度で計算していますから十分良い精度が出ていると思います。
このように、新しいアルゴリズムではベクトル\( \boldsymbol{a} \)と\( \boldsymbol{b} \)がどのような位置関係にあっても特異点を生じることなく計算できます。特異点近傍での処理分岐も不要なので実装しやすくて良いですね。
使用したプログラムは以下のリンクからアクセスできます。
https://github.com/HamaguRe/space-denpa_analysis_rotate_a_to_b